Как доказать существование бога с помощью логики и математики?

На протяжении веков несколько математиков неоднократно пытались доказать существование божественного существа: от Блеза Паскаля и Рене Декарта (в XVII веке) до Готфрида Вильгельма Лейбница (в XVIII веке) и Курта Гёделя (в XX веке). Удивительная вещь: в предварительном исследовании, впервые опубликованном в 2013 году, мастер алгоритмических доказательств проверил логическую цепочку рассуждений Гёделя и обнаружил, что она несомненно верна. Разбираемся, как математика способна опровергнуть главное утверждение всех атеистов.

Лейбниц, Декарт и Гёдель полагались на онтологическое доказательство бога, в котором они выводили его существование из логических выводов. Паскаль (1623-1662) выбрал несколько иной подход. Он анализировал проблему с точки зрения того, что сегодня можно было бы считать теорией игр.

Для этого он рассмотрел две возможности. Во-первых, бог существует. Во-вторых, бога не существует. Затем он исследовал последствия веры или неверия. Если бог существует и человек верит в него, он попадает в рай. В противном случае отправится в ад. С другой стороны, если бога нет, ничего не произойдет — независимо от того, религиозны вы или нет. Самая выгодная стратегия, утверждает Паскаль, — это верить в бога. В лучшем случае вы попадете в рай. В худшем вообще ничего не произойдет. Но если же вы не верите, то в худшем случае можете оказаться в аду.

Мысли Паскаля понятны, но они относятся к сценариям из религиозных писаний и не являются доказательством существования высшего существа. Они только говорят, что нужно присоединяться к вере, основанной на оппортунизме.

Богослов и философ Ансельм Кентерберийский (1033-1109) описывал бога как существо, выше которого нельзя помыслить ничего большего. Но если бога нет, то можно вообразить нечто большее, а именно существо, выше которого нельзя созерцать ничего большего. Но, как и бог, это существо также живет и проявляет свойство предельного величия. Вот только эта идея абсурдна: выше самого величайшего, что только можно себе представить, ничего быть не может. Соответственно, предположение о том, что бога не существует, должно быть неверным. Иначе говоря, бог существует.

Потребовалось несколько столетий, чтобы к этой идее обратился не кто иной, как Декарт (1596-1650). Он предоставил почти идентичный аргумент в пользу божественного существования совершенного организма.

Лейбниц (1646-1716) взялся за эту работу несколькими десятилетиями позже и нашел в ней недостатки: Декарт, как он утверждал, не показал, что совершенные свойства определенных сущностей совместимы. Лейбниц продолжал утверждать, что совершенство нельзя исследовать должным образом. Поэтому нельзя опровергнуть то, что совершенные свойства соединяются только в одном существе. Таким образом, возможность божественного существа должна быть реальной. Другими словами, из аргументов Ансельма и Декарта следует, что бог существует.

Однако с математической точки зрения эти мысленные эксперименты стали действительно серьезными только благодаря усилиям Гёделя.

Уже в 25 лет Гёдель перевернул этот вопрос с ног на голову, показав, что математика всегда содержит истинные утверждения, которые невозможно доказать. При этом он использовал логику. Эта же логика также позволила ему доказать существование бога. Гёдель использовал 12 шагов, состоящие из набора аксиом (Ax), теорем (Th) и определений (Df).

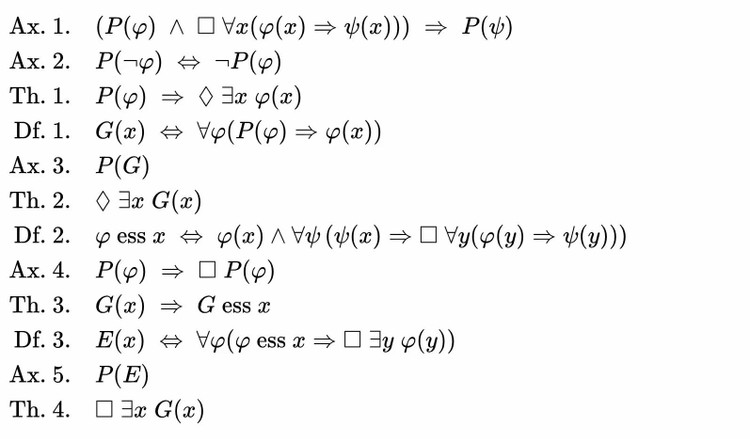
На первый взгляд описанное выше кажется сложным и непонятным. Но давайте пройдемся по строчкам шаг за шагом, следуя мысли Гёделя.

Ученый начинает с аксиомы — допущения: если φ обладает свойством P и из φ всегда следует ψ, то ψ также обладает свойством P. Для простоты можно предположить, что P означает «положительный». Например: если фрукт вкусный (положительное свойство), то его и есть приятно. Таким образом, удовольствие от еды также является положительным свойством.

Вторая аксиома устанавливает дополнительные рамки для P. Если противоположность чему-то положительна, то это «что-то» должно быть отрицательным. Таким образом, Гёдель разделил мир на черное и белое: либо что-то хорошо, либо что-то плохо. Например, если здоровье хорошее, то болезнь обязательно должна быть плохой.

Используя эти две посылки, Гёдель выводит первую теорему: если φ — положительное свойство, то существует вероятность существования x со свойством φ. То есть возможно существование положительных вещей.

Затем математик впервые обращается к определению божественного существа: x является божественным, если оно обладает всеми положительными свойствами φ. Вторая аксиома гарантирует, что бог, определенный таким образом, не может иметь отрицательных характеристик (иначе возникло бы противоречие).

Третья аксиома утверждает, что божественность — это положительная характеристика. Этот пункт не подлежит сомнению, поскольку божественность сочетает в себе абсолютно все хорошее в этом мире.

Вторая теорема становится немного более конкретной: путем объединения третьей аксиомы (божественность положительна) и первой теоремы (существует возможность существования чего-то положительного) существо х может числиться как божественное.

Затем Гёдель пытается показать, что бог обязательно должен существовать в изложенных рамках. Для этого он вводит во второе определение «сущность» φ объекта х, характеристическое свойство, определяющее все остальные характеристики. Наглядный пример — если что-то обладает свойством вкусности, то оно обязательно хорошо приготовлено.

Четвертая аксиома утверждает, что если что-то положительно, то оно всегда положительно — независимо от времени, ситуации или места.

После этого Гёдель формулирует третью теорему: если существо x божественно, то божественность является его свойством. Это имеет смысл, потому что если что-то божественно, оно обладает всеми положительными характеристиками — и, таким образом, свойства x фиксированы.

Следующий шаг связан с реальностью конкретного существа. Если где-то хотя бы одно существо y обладает свойством φ, которое является свойством x, то x также существует. То есть, если существует что-то красивое, то красота тоже должна существовать.

Согласно пятой аксиоме существование есть положительное свойство. Это очевидно.

Отсюда можно заключить, что бог реален, поскольку это существо обладает всеми положительными свойствами, а существование положительно само по себе.

Как оказалось, все логические выводы Гёделя верны — даже компьютеры смогли это доказать. Тем не менее эти выводы также вызвали критику. Помимо аксиом, которые, конечно, могут быть подвергнуты сомнению (почему мир должен быть разделен на «добро» и «зло»?), Гёдель не дает более подробной информации о том, что такое положительное свойство.

Ученый действительно смог доказать, что существование чего-то, что он определял как божественное, обязательно следует из определенных предположений. Но можно поставить под сомнение их обоснованность.

Например, если мы предполагаем, что все кошки трехцветные, мы знаем, что трехцветные кошки почти всегда самки, то мы можем сделать вывод: почти все кошки — самки.

Даже если логические рассуждения верны, это, конечно, не так. Ибо само предположение, что все кошки трехцветные, ложно. Если кто-то делает заявления о наблюдаемых вещах в нашем окружении, таких как кошки, их можно проверить научными исследованиями. Но если речь идет о доказательстве божественного существования, дело обстоит немного сложнее.

Это не решает окончательный вопрос о реальности одного (или нескольких) божественных существ. Но каждый волен считать так, как ему угодно.

━━━━━

Анастасия Дегтярева