Ваше лицо и галактика: что такое золотое сечение и как увидеть его в мире вокруг
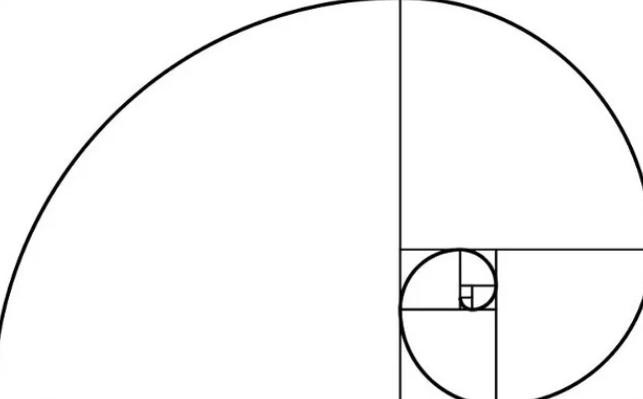
Знаменитая последовательность Фибоначчи веками очаровывала математиков, художников, дизайнеров и ученых. Она начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее до бесконечности. Каждое число является суммой двух предшествующих. В математике соотношение модели равняется 1:0,62. Также известная как золотое сечение, модель нередко можно отыскать вокруг. Закономерности и соотношения присутствуют на микро- и макроуровне, вплоть до биологических систем и неодушевленных объектов. Но правда ли, что сечение использовал Леонардо да Винчи? Можно ли с его помощью определить красоту вашего лица? Разбираемся.
Цветы
Количество лепестков в цветке следует модели Фибоначчи. Посмотрите на лилию с тремя лепестками, лютики с пятью, цикорий с 21, маргаритку с 34 и так далее. Последовательность появляется в лепестках благодаря идеальному расположению, выбранному дарвинистскими процессами. Каждый лепесток находится на 0,618034 оборота (круга 360°), что обеспечивает наилучшее воздействие солнечного света и других факторов.
Головка цветка также подвержена процессам Фибоначчи. Как правило, семена образуются в центре, а затем мигрируют наружу, чтобы заполнить все пространство. Подсолнухи представляют отличный пример этих спиралевидных узоров.
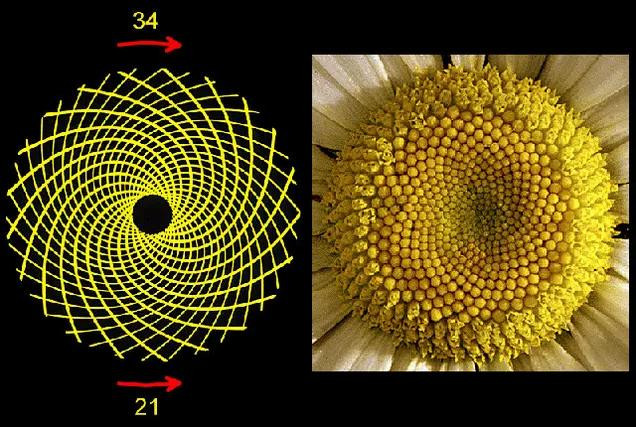
В некоторых случаях семенные головки настолько плотно упакованы, что их общее количество может быть довольно большим — до 144 и более. И при подсчете этих спиралей сумма имеет тенденцию соответствовать числу Фибоначчи.
Ракушки
Еще один пример — уникальные свойства золотого прямоугольника. Эта форма, прямоугольник, в котором отношение сторон a/b равно золотой середине (фи), может привести к процессу, который повторяется до бесконечности и принимает форму логарифмической спирали. Она изобилует в природе.
Раковины улиток и наутилусов следуют логарифмической спирали, как и улитка внутреннего уха человека. Ее также можно увидеть в рогах некоторых коз и в форме паутины некоторых пауков.
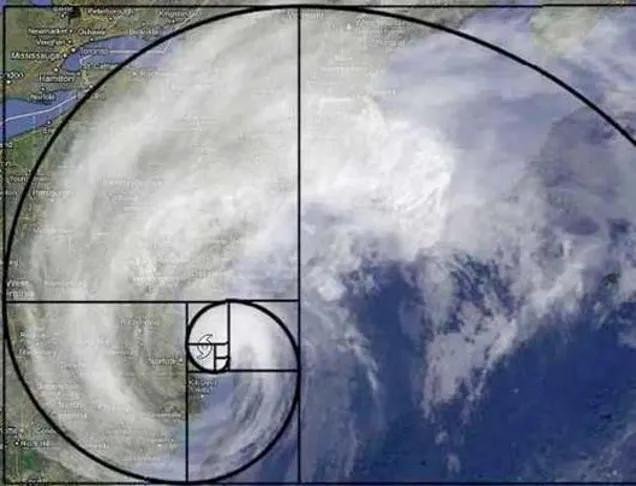
Спиральные галактики и ураганы
Неудивительно, что спиральные галактики также следуют схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет собой логарифмическую спираль с углом наклона около 12°.
Интересно, что спиральные галактики бросают вызов ньютоновской физике. Еще в 1925 году астрономы поняли, что, поскольку угловая скорость вращения галактического диска меняется с расстоянием от центра, радиальные рукава должны искривляться по мере вращения галактик. Впоследствии, после нескольких оборотов, вокруг галактики должны начать закручиваться спиральные рукава. Но они этого не делают — отсюда возникает так называемая проблема намотки. Звезды снаружи движутся со скоростью выше ожидаемой — уникальная черта космоса, помогающая сохранять свою форму.
Ваше лицо
Считается, что рот и нос расположены в золотых секциях на определенном расстоянии между глазами и нижней частью подбородка. Подобные пропорции видны и сбоку.
Важно отметить, что тело каждого человека отличается, но средние значения среди населения имеют тенденцию к модели золотого сечения. Чем ближе наши пропорции соответствуют ей, тем более привлекательными воспринимаются эти черты. Например, некоторые ученые и психологи считают, что самые красивые улыбки — это те, в которых центральные резцы в 1,618 раза шире боковых, которые в 1,618 раза шире клыков, и так далее. Вполне возможно, что с эво-психологической точки зрения мы склонны любить физические формы, соответствующие золотому сечению — потенциальному показателю репродуктивной пригодности и здоровья.
Золотое сечение в искусстве
Золотое сечение повлияло на многие области, включая архитектуру, математику, дизайн и искусство. Некоторые считают, что эти пропорции использовал Леонардо да Винчи для построения собственных шедевров. В картине «Тайная вечеря», например, каждое ключевое измерение комнаты, стола и декораций основывается на золотом сечении, а в эпоху Возрождения оно было известно как божественная пропорция.
Определенным фигурам, например, додекаэдрам и икосаэдрам, присущи золотые пропорции в размерах и пространственном положении их пересекающихся линий. Некоторые художники и архитекторы считают, что золотое сечение создает самые красивые формы.
Во многих книгах утверждается, что если нарисовать прямоугольник вокруг лица Моны Лизы, отношение высоты к ширине будет равно золотому сечению. Некоторые сомневаются в правдивости этого утверждения, поскольку не существует никаких документов, указывающих на то, что Леонардо сознательно использовал сечение в композиции, а также на то, где именно должен быть нарисован прямоугольник. Тем не менее следует признать тот факт, что Леонардо был близким другом Луки Пачоли, опубликовавшего в 1509 году трехтомный трактат о золотом сечении (под названием Divina Proportione). Возможно, именно идеи Пачоли сильно повлияли на великого художника.
Одним из самых известных подобных примеров является Витрувианский человек. Однако пропорции на этой картине не соответствуют золотому сечению. Действительно, в своих работах Леонардо упоминал только отношения целых чисел.
Золотого сечения не существует?
Считается, что можно наложить на красивое лицо всевозможные прямоугольники, а затем заявить, что красота происходит от его пропорций. Однако с этим согласны не все. Некоторые математики утверждают, что у тела есть много возможных соотношений, многие из которых находятся где-то между 1 и 2. Если учесть мелкие детали, вы обязательно получите числа, близкие к значению золотого сечения (около 1,618). Это особенно верно, если измеряемые вещи не очень четко определены и можно варьировать определение таким образом, чтобы получить пропорции, которые вы хотите найти.
Если взглянуть достаточно внимательно, вы также увидите пропорции в человеческом теле, близкие к 1,6; 5/3, 3/2, квадратному корню из 2, 42/26 и так далее. Действительно, у большинства чисел между 1 и 2 будет две части тела, приближающиеся к ним в соотношении. Но, поскольку золотое сечение является иррациональным числом, вы никогда не увидите его точно ни в каком измерении.
Все это — пример того, как человеческий мозг находит ложные корреляции. Действительно, при наличии достаточного количества данных можно найти закономерности, которые согласуются практически с любой гипотезой. Хороший способ убедиться в этом — выйти на улицу в погожий солнечный день и посмотреть на облака. Рано или поздно вы найдете облако, которое соответствует какой-то новой модели, а не золотому сечению.
Доказательств того, что золотой прямоугольник особенно приятен, довольно мало. Психологические исследования, демонстрирующие различные прямоугольники для групп людей, по-видимому, указывают на то, что существовал широкий диапазон предпочтений. При этом отношение квадратного корня из двух к одному часто предпочтительнее, чем другие.
Популяризацию золотого сечения приписывают Адольфу Цейзингу, немецкому психологу XIX века, который считал его универсальным законом, описывающим «красоту и полноту в царствах как природы, так и искусства [...], которые пронизывают, как высший духовный идеал, все структуры, формы и пропорции, будь то космические или индивидуальные, органические или неорганические, акустические или оптические». Это лишь пример наблюдения ложных паттернов. Однако работа Цейзинга повлияла на многих и заложила основы большей части современного мифа.
Последовательность Фибоначчи, безусловно, существует в природе, поскольку она связана как с тем, как растет население, так и с тем, как формы могут соединяться друг с другом. Но в стойких мифах о повсеместном золотом сечении таится опасность. Школьников и многих других вводят в ложную реальность о том, как работает математика. Рано или поздно они обнаружат, что эта реальность не соответствует действительности, и потеряют веру в вполне реальную способность математики объяснять мир.
━━━━━
Анастасия Дегтярева